《PostgreSQL技术内幕——原理探索》第三章 查询处理

查询处理是PostgreSQL中最为复杂的子系统。如PostgreSQL官方文档所述，PostgreSQL支持SQL2011标准中的大多数特性，查询处理子系统能够高效地处理这些SQL。本章概述了查询处理的流程，特别关注了查询优化的部分。

本章包括下列三个部分：

• 第一部分：3.1节

  这一节会简单介绍PostgreSQL中查询处理的流程。

• 第二部分：3.2~3.4节

  这一部分会描述获取单表查询上最优执行计划的步骤。3.2节讨论代价估计的过程，3.3节描述创建计划树的过程，3.4节将简要介绍执行器的工作过程。

• 第三部分：3.5~3.6节

  这一部分会描述获取多表查询上最优执行计划的步骤。3.5节介绍了三种连接算法：嵌套循环连接（Nested Loop Join），归并连接（Merge Join） ，散列连接（Hash Join）。3.6节将介绍为多表查询创建计划树的过程。

PostgreSQL支持三种技术上很有趣，而且也很实用的功能：外部数据包装（Foreign Data Wrapper, FDW），并行查询，以及版本11即将支持的JIT编译。前两者将在第4章中描述，JIT编译超出范围本书的范围，详见官方文档。

3.1 概览

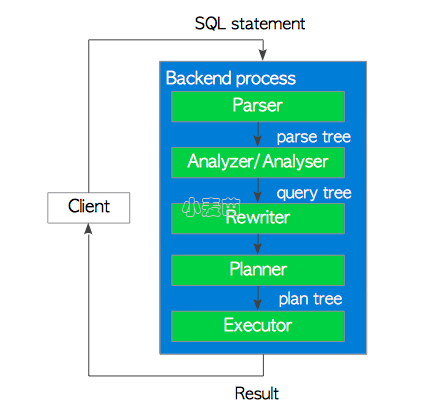
尽管PostgreSQL在9.6版本后有了基于多个后台工作进程的并行查询，但大体上来讲，还是每个连接对应一个后端进程。后端进程由五个子系统组成，如下所示：

1. 解析器（Parser）

   解析器根据SQL语句生成一颗语法解析树（parse tree） 。

2. 分析器（Analyzer）

   分析器对语法解析树进行语义分析，生成一颗查询树（query tree）。

3. 重写器（Rewriter）

   重写器按照规则系统中存在的规则，对查询树进行改写。

4. 计划器（Planner）

   计划器基于查询树，生成一颗执行效率最高的计划树（plan tree）。

5. 执行器（Executor）

   执行器按照计划树中的顺序访问表和索引，执行相应查询。

图3.1 查询处理

本节将概述这些子系统。计划器和执行器很复杂，后面的章节会对这些函数的细节进行描述。

PostgreSQL的查询处理在官方文档中有详细的描述

3.1.1 解析器（Parser）

解析器基于SQL语句的文本，生成一颗后续子系统可以理解的语法解析树。下面是一个具体的例子。

考虑以下查询：

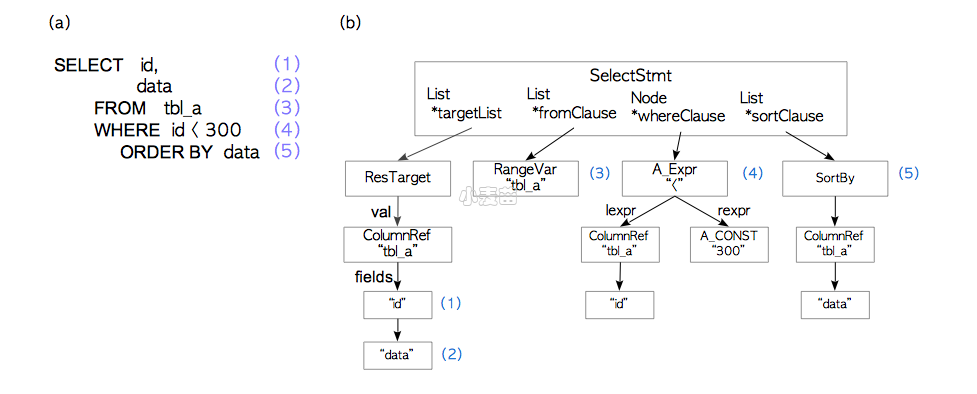
语法解析树的根节点是一个定义在parsenodes.h中的SelectStmt数据结构。图3.2(a)展示了一个查询，而图3.2(b)则是该查询对应的语法解析树。

图3.2. 语法解析树的例子

SELECT查询中的元素和语法解析树中的元素有着对应关系。比如，(1)是目标列表中的一个元素，与目标表的'id'列相对应，(4)是一个WHERE子句，诸如此类。

当解析器生成语法分析树时只会检查语法，只有当查询中出现语法错误时才会返回错误。解析器并不会检查输入查询的语义，举个例子，如果查询中包含一个不存在的表名，解析器并不会报错，语义检查由分析器负责。

3.1.2 分析器（Analyzer）

分析器对解析器产出的语法解析树（parse tree）进行语义分析，并产出一颗查询树（query tree）。

查询树的根节点是parsenode.h中定义的Query数据结构，这个结构包含着对应查询的元数据，比如命令的类型（SELECT/INSERT等），还包括了一些叶子节点，叶子节点由列表或树组成，包含了特定子句相应的数据。

图3.3 查询树一例

简要介绍一下上图中的查询树：

• targetlist 是查询结果中列（Column）的列表。在本例中该列表包含两列：id 和data。如果在输入的查询树中使用了*（星号），那么分析器会将其显式替换为所有具体的列。
• 范围表rtable是该查询所用到关系的列表。本例中该变量包含了表tbl_a的信息，如该表的表名与oid。
• 连接树jointree存储着FROM和WHERE子句的相关信息。
• 排序子句sortClause是SortGroupClause结构体的列表。

官方文档描述了查询树的细节。

3.1.3 重写器（Rewriter）

PostgreSQL的规则系统正是基于重写器实现的；当需要时，重写器会根据存储在pg_rules中的规则对查询树进行转换。规则系统本身也是一个很有趣的系统，不过本章略去了关于规则系统和重写器的描述，以免内容过于冗长。

视图

在PostgreSQL中，视图是基于规则系统实现的。当使用CREATE VIEW命令定义一个视图时，PostgreSQL就会创建相应的规则，并存储到系统目录中。

假设下面的视图已经被定义，而pg_rule中也存储了相应的规则。

sampledb=# CREATE VIEW employees_list sampledb-# AS SELECT e.id, e.name, d.name AS department sampledb-# FROM employees AS e, departments AS d WHERE e.department_id = d.id;

1 2 3

sampledb=# CREATE VIEW employees_list sampledb-#   AS SELECT e.id, e.name, d.name AS department sampledb-#      FROM employees AS e, departments AS d WHERE e.department_id = d.id;

当执行一个包含该视图的查询，解析器会创建一颗如图3.4(a)所示的语法解析树。

sampledb=# SELECT * FROM employees_list;

1	sampledb=# SELECT * FROM employees_list;

在该阶段，重写器会基于pg_rules中存储的视图规则将rangetable节点重写为一颗查询子树，与子查询相对应。

图3.4 重写阶段一例

因为PostgreSQL使用这种机制实现视图，直到9.2版本，视图都是不能更新的。虽然9.3版本后可以对视图进行更新，但对视图的更新仍然存在很多限制，具体细节请参考官方文档。

3.1.4 计划器与执行器

计划器从重写器获取一颗查询树（query tree），基于查询树生成一颗能被执行器高效执行的（查询）计划树（plan tree）。

在PostgreSQL中，计划器是完全基于代价估计（cost-based）的；它不支持基于规则的优化与提示（hint）。计划器是RDBMS中最为复杂的部分，因此本章的后续内容会对计划器做一个概述。

pg_hint_plan

PostgreSQL不支持SQL中的提示（hint），并且永远也不会去支持。如果你想在查询中使用提示，可以考虑使用pg_hint_plan扩展，细节请参考官方站点。

与其他RDBMS类似，PostgreSQL中的EXPLAIN命令会显示命令的计划树。下面给出了一个具体的例子。

图3.5展示了结果相应的计划树。

图3.5 一个简单的计划树以及其与EXPLAIN命令的关系

计划树由许多称为计划节点（plan node）的元素组成，这些节点挂在PlannedStmt结构对应的计划树上。这些元素的定义在plannodes.h中，第3.3.3节与第3.5.4.2会解释相关细节。

每个计划节点都包含着执行器进行处理所必需的信息，在单表查询的场景中，执行器会按照从终端节点往根节点的顺序依次处理这些节点。

比如图3.5中的计划树就是一个列表，包含一个排序节点和一个顺序扫描节点；因而执行器会首先对表tbl_a执行顺序扫描，并对获取的结果进行排序。

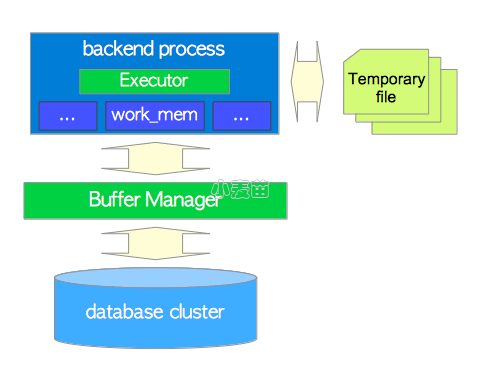
执行器会通过第8章将介绍的缓冲区管理器来访问数据库集簇的表和索引。当处理一个查询时，执行器会使用预先分配的内存空间，比如temp_buffers和work_mem，必要时还会创建临时文件。

图3.6 执行器，缓冲管理器，临时文件之间的关系

除此之外，当访问元组的时候，PostgreSQL还会使用并发控制机制来维护运行中事务的一致性和隔离性。第五章介绍了并发控制机制。

3.2 单表查询的代价估计

PostgreSQL的查询优化是基于代价（Cost）的。代价是一个无量纲的值，它并不是一种绝对的性能指标，但可以作为比较各种操作代价时的相对性能指标。

costsize.c中的函数用于估算各种操作的代价。所有被执行器执行的操作都有着相应的代价函数。例如，函数cost_seqscan() 和 cost_index()分别用于估算顺序扫描和索引扫描的代价。

在PostgreSQL中有三种代价：启动（start-up） ， 运行（run）和总和（total）。总代价是启动代价和运行代价的和；因此只有启动代价和运行代价是单独估计的。

1. 启动代价（start-up）：在读取到第一条元组前花费的代价，比如索引扫描节点的启动代价就是读取目标表的索引页，取到第一个元组的代价
2. 运行代价（run）： 获取全部元组的代价
3. 总代价（total）：前两者之和

EXPLAIN命令显示了每个操作的启动代价和总代价，下面是一个简单的例子：

在第4行显示了顺序扫描的相关信息。代价部分包含了两个值：0.00和145.00。在本例中，启动代价和总代价分别为0.00和145.00。

在本节中，我们将详细介绍顺序扫描，索引扫描和排序操作的代价是如何估算的。

在接下来的内容中，我们使用下面这个表及其索引作为例子。

3.2.1 顺序扫描

顺序扫描的代价是通过函数cost_seqscan()估计的。本节将研究顺序扫描代价是如何估计的，以下面的查询为例：

在顺序扫描中，启动代价等于0，而运行代价由以下公式定义： $$ \begin{align} \verb|run_cost| &= \verb|cpu_run_cost| + \verb|disk_run_cost | \ &= (\verb|cpu_tuple_cost| + \verb|cpu_operatorcost|) × N{\verb|tuple|} + \verb|seq_pagecost| × N{\verb|page|}, \end{align} $$ 其中seq_page_cost，cpu_tuple_cost和cpu_operator_cost是在postgresql.conf 中配置的参数，默认值分别为1.0，0.01和0.0025。$N{\verb|tuple|}$ 和$N{\verb|page|}$ 分别是表中的元组总数与页面总数，这两个值可以使用以下查询获取。

$$ \begin{equation}\tag{1} N_{\verb|tuple|}=10000 \end{equation} $$

$$ \begin{equation}\tag{2} N_{\verb|page|}=45 \end{equation} $$

因此： $$ \begin{align} \verb|run_cost| &= (0.01 + 0.0025) × 10000 + 1.0 × 45 = 170.0. \end{align} $$

最终： $$ \verb|total_cost| = 0.0 + 170.0 = 170.0 $$

作为验证，下面是该查询的EXPLAIN结果：

在第4行中可以看到，启动代价和总代价分别是0.00和170.0，且预计全表扫描返回行数为8000条（元组）。

在第5行显示了一个顺序扫描的过滤器Filter:(id < 8000)。更精确地说，它是一个表级过滤谓词（table level filter predicate）。注意这种类型的过滤器只会在读取所有元组的时候使用，它并不会减少需要扫描的表页面数量。

从优化运行代价的角度来看，PostgreSQL假设所有的物理页都是从存储介质中获取的；即，PostgreSQL不会考虑扫 描的页面是否来自共享缓冲区。

3.2.2 索引扫描

尽管PostgreSQL支持很多索引方法，比如B树，GiST，GIN和BRIN，不过索引扫描的代价估计都使用一个共用的代价函数：cost_index()。

本节将研究索引扫描的代价是如何估计的，以下列查询为例。

在估计该查询的代价之前，下面的查询能获取$N{\verb|index|,\verb|page|}$和$N{\verb|index|,\verb|tuple|}$的值：

$$ \begin{equation}\tag{3} N_{\verb|index|,\verb|tuple|} = 10000 \end{equation} $$

$$ \begin{equation}\tag{4} N_{\verb|index|,\verb|page|} = 30 \end{equation} $$

3.2.2.1 启动代价

索引扫描的启动代价就是读取索引页以访问目标表的第一条元组的代价，由下面的公式定义： $$ \begin{equation} \verb| start-up_cost| = {\mathrm{ceil}(\log2 (N{\verb|index|,\verb|tuple|})) + (H_{\verb|index|} + 1) × 50} × \verb|cpu_operatorcost| \end{equation} $$ 其中$H{\verb|index|}$是索引树的高度。

在本例中，套用公式(3)，$N{\verb|index,tuple|}$是10000；$H{\verb|index|}$是1；$\verb|cpu_operator_cost|$是0.0025（默认值）。因此 $$ \begin{equation}\tag{5} \verb|start-up_cost| = {\mathrm{ceil}(\log_2(10000)) + (1 + 1) × 50} × 0.0025 = 0.285 \end{equation} $$

3.2.2.2 运行代价

索引扫描的运行代价是表和索引的CPU代价与IO代价之和。 $$ \begin{align} \verb|run_cost| &= (\verb|index_cpu_cost| + \verb|table_cpu_cost|) + (\verb|index_io_cost| + \verb|table_io_cost|). \end{align} $$

如果使用仅索引扫描，则不会估计table_cpu_cost与table_io_cost，仅索引扫描将在第七章中介绍。

前三个代价（即index_cpu_cost，table_cpu_cost和index_io_cost）如下所示：

$$ \begin{align} \verb|index_cpucost| &= \verb|Selectivity| × N{\verb|index|,\verb|tuple|} × (\verb|cpu_index_tuple_cost| + \verb|qual_op_cost|) \ \verb|table_cpucost| &= \verb|Selectivity| × N{\verb|tuple|}× \verb|cpu_tuple_cost| \ \verb|index_iocost| &= \mathrm{ceil}(\verb|Selectivity| × N{\verb|index|,\verb|page|}) ×\verb|random_page_cost| \end{align} $$

以上公式中的cpu_index_tuple_cost和random_page_cost在postgresql.conf中配置（默认值分别为0.005和4.0）。$\verb|qual_op_cost|$粗略来说就是索引求值的代价，默认值是0.0025，这里不再展开。选择率（Selectivity）是一个0到1之间的浮点数，代表查询指定的MARKDOWN_HASH5105e0481cb9b1e1d0dd3e10bab1f1c0MARKDOWNHASH子句在索引中搜索范围的比例。举个例子，$(\verb|Selectivity| × N{\verb|tuple|})$就是需要读取的表元组数量，$(\verb|Selectivity| × N_{\verb|index|,\verb|tuple|})$就是需要读取的索引元组数量，诸如此类。

选择率（Selectivity）

查询谓词的选择率是通过直方图界值（histogram_bounds）与高频值（Most Common Value, MCV）估计的，这些信息都存储在系统目录pg_statistics中，并可通过pg_stats视图查询。这里通过一个具体的例子来简要介绍选择率的计算方法，细节可以参考官方文档。

表中每一列的高频值都在pg_stats视图的most_common_vals和most_common_freqs中成对存储。

• 高频值（most_common_vals）：该列上最常出现的取值列表
• 高频值频率（most_common_freqs）：高频值相应出现频率的列表

下面是一个简单的例子。表countries有两列：一列country存储国家名，一列continent存储该国所属大洲。

testdb=# \d countries Table "public.countries" Column | Type | Modifiers -----------+------+----------- country | text | continent | text | Indexes: "continent_idx" btree (continent) testdb=# SELECT continent, count(*) AS "number of countries", testdb-# (count(*)/(SELECT count(*) FROM countries)::real) AS "number of countries / all countries" testdb-# FROM countries GROUP BY continent ORDER BY "number of countries" DESC; continent | number of countries | number of countries / all countries ---------------+---------------------+------------------------------------- Africa | 53 | 0.274611398963731 Europe | 47 | 0.243523316062176 Asia | 44 | 0.227979274611399 North America | 23 | 0.119170984455959 Oceania | 14 | 0.0725388601036269 South America | 12 | 0.0621761658031088 (6 rows)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

testdb=# \d countries    Table "public.countries"   Column   | Type | Modifiers -----------+------+----------- country   | text | continent | text | Indexes:     "continent_idx" btree (continent)   testdb=# SELECT continent, count(*) AS "number of countries", testdb-#     (count(*)/(SELECT count(*) FROM countries)::real) AS "number of countries / all countries" testdb-#       FROM countries GROUP BY continent ORDER BY "number of countries" DESC;    continent   | number of countries | number of countries / all countries ---------------+---------------------+------------------------------------- Africa        |                  53 |                   0.274611398963731 Europe        |                  47 |                   0.243523316062176 Asia          |                  44 |                   0.227979274611399 North America |                  23 |                   0.119170984455959 Oceania       |                  14 |                  0.0725388601036269 South America |                  12 |                  0.0621761658031088 (6 rows)

考虑下面的查询，该查询带有WHERE条件continent = 'Asia'。

testdb=# SELECT * FROM countries WHERE continent = 'Asia';

1	testdb=# SELECT * FROM countries WHERE continent = 'Asia';

这时候，计划器使用continent列上的高频值来估计索引扫描的代价，列上的most_common_vals与 most_common_freqs如下所示：

testdb=# \x Expanded display is on. testdb=# SELECT most_common_vals, most_common_freqs FROM pg_stats testdb-# WHERE tablename = 'countries' AND attname='continent'; -[ RECORD 1 ]-----+----------------------------------------------------------- most_common_vals | {Africa,Europe,Asia,"North America",Oceania,"South America"} most_common_freqs | {0.274611,0.243523,0.227979,0.119171,0.0725389,0.0621762}

1 2 3 4 5 6 7

testdb=# \x Expanded display is on. testdb=# SELECT most_common_vals, most_common_freqs FROM pg_stats testdb-#                  WHERE tablename = 'countries' AND attname='continent'; -[ RECORD 1 ]-----+----------------------------------------------------------- most_common_vals  | {Africa,Europe,Asia,"North America",Oceania,"South America"} most_common_freqs | {0.274611,0.243523,0.227979,0.119171,0.0725389,0.0621762}

与most_common_vals中Asia值对应的most_common_freqs为0.227979。因此0.227979会在估算中被用作选择率。

如果高频值不可用，就会使用目标列上的直方图界值来估计代价。

• 直方图值（histogram_bounds）是一系列值，这些值将列上的取值划分为数量大致相同的若干个组。

下面是一个具体的例子。这是表tbl中data列上的直方图界值；

testdb=# SELECT histogram_bounds FROM pg_stats WHERE tablename = 'tbl' AND attname = 'data'; histogram_bounds ------------------------------------------------------------------------------ {1,100,200,300,400,500,600,700,800,900,1000,1100,1200,1300,1400,1500,1600,1700,1800,1900,2000,2100, 2200,2300,2400,2500,2600,2700,2800,2900,3000,3100,3200,3300,3400,3500,3600,3700,3800,3900,4000,4100, 4200,4300,4400,4500,4600,4700,4800,4900,5000,5100,5200,5300,5400,5500,5600,5700,5800,5900,6000,6100, 6200,6300,6400,6500,6600,6700,6800,6900,7000,7100,7200,7300,7400,7500,7600,7700,7800,7900,8000,8100, 8200,8300,8400,8500,8600,8700,8800,8900,9000,9100,9200,9300,9400,9500,9600,9700,9800,9900,10000} (1 row)

1 2 3 4 5 6 7 8 9

testdb=# SELECT histogram_bounds FROM pg_stats WHERE tablename = 'tbl' AND attname = 'data';                                    histogram_bounds ------------------------------------------------------------------------------ {1,100,200,300,400,500,600,700,800,900,1000,1100,1200,1300,1400,1500,1600,1700,1800,1900,2000,2100, 2200,2300,2400,2500,2600,2700,2800,2900,3000,3100,3200,3300,3400,3500,3600,3700,3800,3900,4000,4100, 4200,4300,4400,4500,4600,4700,4800,4900,5000,5100,5200,5300,5400,5500,5600,5700,5800,5900,6000,6100, 6200,6300,6400,6500,6600,6700,6800,6900,7000,7100,7200,7300,7400,7500,7600,7700,7800,7900,8000,8100, 8200,8300,8400,8500,8600,8700,8800,8900,9000,9100,9200,9300,9400,9500,9600,9700,9800,9900,10000} (1 row)

默认情况下，直方图界值会将列上的取值划分入100个桶。图3.7展示了这些桶及其对应的直方图界值。桶从0开始编号，每个桶保存了（大致）相同数量的元组。直方图界值就是相应桶的边界。比如，直方图界值的第0个值是1，意即这是bucket_0中的最小值。第1个值是100，意即bucket_1中的最小值是100，等等。

图3.7 桶和直方图界值

然后本节例子中选择率计算如下所示。假设查询带有WHERE子句data < 240，而值240落在第二个桶中。在本例中可以通过线性插值推算出相应的选择率。因此查询中data列的选择率可以套用下面的公式计算： $$ \verb|Selectivity| = \frac{2+(240-hb[2])/(hb[3]-hb[2])}{100}=\frac{2+(240-200)/(300-200)}{100}=\frac{2+40/100}{100}=0.024 \ (6) $$

因此，根据公式(1)，(3)，(4)和(6)，有 $$ \begin{equation}\tag{7} \verb|index_cpu_cost| = 0.024× 10000 × (0.005+0.0025)=1.8 \end{equation} $$ $$ \begin{equation}\tag{8} \verb|table_cpu_cost| = 0.024 × 10000 × 0.01 = 2.4 \end{equation} $$

$$ \begin{equation}\tag{9} \verb|index_io_cost| = \mathrm{ceil}(0.024 × 30) × 4.0 = 4.0 \end{equation} $$

$\verb|table_io_cost|$ 由下面的公式定义： $$ \begin{equation} \verb|table_io_cost| = \verb|max_io_cost| + \verb|indexCorerelation|^2 × (\verb|min_io_cost|-\verb|max_io_cost|) \end{equation} $$

$\verb|max_io_cost_io_cost|$ 是最差情况下的I/O代价，即，随机扫描所有数据页的代价；这个代价由以下公式定义： $$ \begin{equation} \verb|max_iocost| = N{\verb|page|} × \verb|random_page_cost| \end{equation} $$

在本例中，由(2)，$N_{\verb|page|}=45$，得 $$ \begin{equation}\tag{10} \verb|max_io_cost| = 45 × 4.0 = 180.0 \end{equation} $$

$\verb|min_io_cost|$是最优情况下的I/O代价，即，顺序扫描选定的数据页；这个代价由以下公式定义： $$ \begin{equation} \verb|min_io_cost| = 1 × \verb|random_pagecost| + (\mathrm{ceil}(\verb|Selectivity| × N{\verb|page|})-1) × \verb|seq_page_cost| \end{equation} $$ 在本例中， $$ \begin{equation} \tag{11} \verb|min_io_cost| \ = 1 × 4.0 + (\mathrm{ceil}(0.024 × 45)-1) × 1.0 \end{equation} $$

下文详细介绍$\verb|indexCorrelation|$，在本例中， $$ \begin{equation} \tag{12} \verb|indexCorrelation| = 1.0 \end{equation} $$

由(10)，(11)和(12)，得 $$ \begin{equation} \tag{13} \verb|table_io_cost| = 180.0+1.0^2 × (5.0-180.0)=5.0 \end{equation} $$

综上，由(7)，(8)，(9)和(13)得 $$ \begin{equation}\tag{14} \verb|run_cost| = (1.8+2.4)+(4.0+5.0)=13.2 \end{equation} $$

索引相关性（index correlation）

索引相关性是列值在物理上的顺序和逻辑上的顺序的统计相关性（引自官方文档）。索引相关性的取值范围从$-1$到$+1$。下面的例子有助于理解索引扫描和索引相关性的关系。

表tbl_corr有5个列：两个列为文本类型，三个列为整数类型。这三个整数列保存着从1到12的数字。在物理上表tbl_corr包含三个页，每页有4条元组。每个数字列有一个名如index_col_asc的索引。

testdb=# \d tbl_corr Table "public.tbl_corr" Column | Type | Modifiers ----------+---------+----------- col | text | col_asc | integer | col_desc | integer | col_rand | integer | data | text | Indexes: "tbl_corr_asc_idx" btree (col_asc) "tbl_corr_desc_idx" btree (col_desc) "tbl_corr_rand_idx" btree (col_rand) testdb=# SELECT col,col_asc,col_desc,col_rand testdb-# FROM tbl_corr; col | col_asc | col_desc | col_rand ----------+---------+----------+---------- Tuple_1 | 1 | 12 | 3 Tuple_2 | 2 | 11 | 8 Tuple_3 | 3 | 10 | 5 Tuple_4 | 4 | 9 | 9 Tuple_5 | 5 | 8 | 7 Tuple_6 | 6 | 7 | 2 Tuple_7 | 7 | 6 | 10 Tuple_8 | 8 | 5 | 11 Tuple_9 | 9 | 4 | 4 Tuple_10 | 10 | 3 | 1 Tuple_11 | 11 | 2 | 12 Tuple_12 | 12 | 1 | 6 (12 rows)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

testdb=# \d tbl_corr     Table "public.tbl_corr"   Column  |  Type   | Modifiers ----------+---------+----------- col      | text    | col_asc  | integer | col_desc | integer | col_rand | integer | data     | text    | Indexes:     "tbl_corr_asc_idx" btree (col_asc)     "tbl_corr_desc_idx" btree (col_desc)     "tbl_corr_rand_idx" btree (col_rand) testdb=# SELECT col,col_asc,col_desc,col_rand testdb-#                         FROM tbl_corr;    col    | col_asc | col_desc | col_rand ----------+---------+----------+---------- Tuple_1  |       1 |       12 |        3 Tuple_2  |       2 |       11 |        8 Tuple_3  |       3 |       10 |        5 Tuple_4  |       4 |        9 |        9 Tuple_5  |       5 |        8 |        7 Tuple_6  |       6 |        7 |        2 Tuple_7  |       7 |        6 |       10 Tuple_8  |       8 |        5 |       11 Tuple_9  |       9 |        4 |        4 Tuple_10 |      10 |        3 |        1 Tuple_11 |      11 |        2 |       12 Tuple_12 |      12 |        1 |        6 (12 rows)

这些列的索引相关性如下：

testdb=# SELECT tablename,attname, correlation FROM pg_stats WHERE tablename = 'tbl_corr'; tablename | attname | correlation -----------+----------+------------- tbl_corr | col_asc | 1 tbl_corr | col_desc | -1 tbl_corr | col_rand | 0.125874 (3 rows)

1 2 3 4 5 6 7

testdb=# SELECT tablename,attname, correlation FROM pg_stats WHERE tablename = 'tbl_corr'; tablename | attname  | correlation -----------+----------+------------- tbl_corr  | col_asc  |           1 tbl_corr  | col_desc |          -1 tbl_corr  | col_rand |    0.125874 (3 rows)

当执行下列查询时，由于所有的目标元组都在第一页中，PostgreSQL只会读取第一页，如图3.8(a)所示。

testdb=# SELECT * FROM tbl_corr WHERE col_asc BETWEEN 2 AND 4;

1	testdb=# SELECT * FROM tbl_corr WHERE col_asc BETWEEN 2 AND 4;

而执行下列查询时则不然，PostgreSQL需要读所有的页，如图3.8(b)所示。

testdb=# SELECT * FROM tbl_corr WHERE col_rand BETWEEN 2 AND 4;

1	testdb=# SELECT * FROM tbl_corr WHERE col_rand BETWEEN 2 AND 4;

如此可知，索引相关性是一种统计上的相关性。在索引扫描代价估计中，索引相关性体现了索引顺序和物理元组顺序扭曲程度给随机访问性能造成的影响大小。

图3.8 索引相关性

3.2.2.3 整体代价

由(3)和(14)可得 $$ \begin{equation}\tag{15} \verb|total_cost| = 0.285 + 13.2 = 13.485 \end{equation} $$

作为确认，上述SELECT查询的EXPLAIN结果如下所示：

在第4行可以看到启动代价和总代价分别是0.29和13.49，预估有240条元组被扫描。

在第5行显示了一个索引条件Index Cond:(data < 240)。更准确地说，这个条件叫做访问谓词（access predicate），它表达了索引扫描的开始条件与结束条件。

根据这篇文章，PostgreSQL中的EXPLAIN命令不会区分访问谓词（access predicate）和索引过滤谓词（index filter predicate）。因此当分析EXPLAIN的输出时，即使看到了“IndexCond”，也应当注意一下预估返回行数。

seq_page_cost和random_page_cost

seq_page_cost和random_page_cost的默认值分别为1.0和4.0。这意味着PostgreSQL假设随机扫描比顺序扫描慢4倍；显然，PostgreSQL的默认值是基于HDD（普通硬盘）设置的。

另一方面，近年来SSD得到了广泛的应用，random_page_cost的默认值就显得太大了。使用SSD时如果仍然采用random_page_cost的默认值，则计划器有可能会选择低效的计划。因此当使用SSD时最好将random_page_cost的值设为1.0。

这篇文章报告了使用random_page_cost默认值导致的问题。

3.2.3 排序

排序路径（sort path） 会在排序操作中被使用。排序操作包括ORDER BY，归并连接的预处理操作，以及其他函数。函数cost_sort()用于估计排序操作的代价。

如果能在工作内存中放下所有元组，那么排序操作会选用快速排序算法。否则的话则会创建临时文件，使用文件归并排序算法。

排序路径的启动代价就是对目标表的排序代价，因此代价就是$O(N_{\verb|sort|}× \log2(N{\verb|sort|})$，这里$N{\verb|sort|}$就是待排序的元组数。排序路径的运行代价就是读取已经排好序的元组的代价，因而代价就是$O(N{sort})$。

本节将研究以下查询排序代价的估计过程。假设该查询只使用工作内存，不使用临时文件。

在本例中，启动代价由以下公式定义： $$ \begin{equation} \verb|start-up_cost| = \verb|C|+ \verb|comparisoncost| × N{\verb|sort|} × \log2(N{\verb|sort|}) \end{equation} $$

这里$C$就是上一次扫描的总代价，即上次索引扫描的总代价；由(15)可得C等于13.485；$N_{\verb|sort|}=240$；$\verb|comparison_cost|$ 定义为$2 × \verb|cpu_operator_cost|$。因此有

$$ \begin{equation} \verb|start-up_cost| = 13.485+(2×0.0025)×240.0×\log_2(240.0)=22.973 \end{equation} $$

运行代价是在内存中读取排好序的元组的代价，即： $$ \begin{equation} \verb|run_cost| = \verb|cpu_operatorcost| × N{\verb|sort|} = 0.0025 × 240 = 0.6 \end{equation} $$ 综上： $$ \begin{equation} \verb|total_cost|=22.973+0.6=23.573 \end{equation} $$ 作为确认，以上SELECT查询的EXPLAIN命令结果如下：

在第4行可以看到启动代价和运行代价分别为22.97和23.57。

3.3 创建单表查询的计划树

计划器非常复杂，故本节仅描述最简单的情况，即单表查询的计划树创建过程。更复杂的查询，换而言之即多表查询，其计划树创建过程将在第3.6节中阐述。

PostgreSQL中的计划器会执行三个处理步骤：

1. 执行预处理
2. 在所有可能的访问路径中，找出代价最小的访问路径
3. 按照代价最小的路径，创建计划树

访问路径（access path）是估算代价时的处理单元；比如，顺序扫描，索引扫描，排序以及各种连接操作都有其对应的路径。访问路径只在计划器创建查询计划树的时候使用。最基本的访问路径数据结构就是relation.h中定义的Path结构体。它就相当于是顺序扫描。所有其他的访问路径都基于该结构，下面会介绍细节。

计划器为了处理上述步骤，会在内部创建一个PlannerInfo数据结构。在该数据结构中包含着查询树，查询所涉及关系信息，访问路径等等。

本节会通过一个具体的例子，来描述如何基于查询树创建计划树。

3.3.1 预处理

在创建计划树之前，计划器对先PlannerInfo中的查询树进行一些预处理。

预处理有很多步骤，本节只讨论和单表查询处理相关的主要步骤。其他预处理操作将在3.6节中描述。

1. 简化目标列表（target list），LIMIT子句等；

   例如，表达式2+2会被重写为4，这是由clauses.c中eval_const_expressions()函数负责的。

2. 布尔表达式的规范化

   例如，NOT(NOT a)会被重写为a

3. 压平与/或表达式

   SQL标准中的AND/OR是二元操作符；但在PostgreSQL内部它们是多元操作符。而计划器总是会假设所有的嵌套AND/OR都应当被压平。

   这里有一个具体的例子。考虑这样一个布尔表达式(id = 1) OR (id = 2) OR (id = 3)，图3.9(a) 展示了使用二元表达式时的查询树，预处理会将这些二元算子简化压平为一个三元算子，如图3.9(b)所示。

   图3.9. 压平布尔表达式的例子

   

3.3.2 找出代价最小的访问路径

计划器对所有可能的访问路径进行代价估计，然后选择代价最小的那个。具体来说，计划器会执行以下几个步骤：

1. 创建一个RelOptInfo数据结构，存储访问路径及其代价。

   RelOptInfo结构体是通过make_one_rel()函数创建的，并存储于PlannerInfo结构体的simple_rel_array字段中，如图3.10所示。在初始状态时RelOptInfo持有着baserestrictinfo变量，如果存在相应索引，还会持有indexlist变量。baserestrictinfo存储着查询的WHERE子句，而indexlist存储着目标表上相关的索引。

   typedef enum RelOptKind { RELOPT_BASEREL, RELOPT_JOINREL, RELOPT_OTHER_MEMBER_REL, RELOPT_UPPER_REL, RELOPT_DEADREL } RelOptKind; typedef struct RelOptInfo { NodeTag type; RelOptKind reloptkind; /* 本RelOptInfo包含的所有关系 */ Relids relids; /* 基本关系的ID集合 (范围表索引) */ /* 由计划器生成的预估尺寸 */ double rows; /* 预估结果元组数目 */ /* 计划器标记位，每个关系一份 */ bool consider_startup; /* 保留启动代价最低的路径？ */ bool consider_param_startup; /* 同上, 针对参数化路径？ */ bool consider_parallel; /* 考虑并行路径？ */ /* 扫描当前关系的默认结果目标列表 */ struct PathTarget *reltarget; /* Vars/Exprs, 代价, 宽度的列表 */ /* 物化相关信息 */ List *pathlist; /* Path 结构体列表 */ List *ppilist; /* pathlist中使用的ParamPathInfos */ List *partial_pathlist; /* 部分路径 */ struct Path *cheapest_startup_path; struct Path *cheapest_total_path; struct Path *cheapest_unique_path; List *cheapest_parameterized_paths; /* 基础关系与连接关系都需要的 参数化信息 */ /* (参见 lateral_vars 与 lateral_referencers) */ Relids direct_lateral_relids; /* 直接以LATERAL方式引用的关系 */ Relids lateral_relids; /* 关于基础关系的信息 (连接关系不会设置这些字段！) */ Index relid; Oid reltablespace; /* 表空间 */ RTEKind rtekind; /* RELATION, SUBQUERY, 或 FUNCTION */ AttrNumber min_attr; /* 关系属性的最小值 (通常<0) */ AttrNumber max_attr; /* 关系属性的最大值 */ Relids *attr_needed; /* 被索引的数组 [min_attr .. max_attr] */ int32 *attr_widths; /* 被索引的数组 [min_attr .. max_attr] */ List *lateral_vars; /* 关系所引用的LATERAL Vars 与 PHVs */ Relids lateral_referencers;/* 侧面引用本表的关系 */ List *indexlist; /* IndexOptInfo列表 */ BlockNumber pages; /* 来自pg_class的页面数估计值 */ double tuples; double allvisfrac; PlannerInfo *subroot; /* 如有子查询 */ List *subplan_params; /* 如有子查询 */ int rel_parallel_workers; /* 期望的并行工作进程数量 */ /* 有关外部表与外部表连接的相关信息 */ Oid serverid; /* 外部表与外部表连接相应的服务器ID */ Oid userid; /* 用于检查访问权限的用户标识 */ bool useridiscurrent;/* 当前用户是否能合法进行JOIN */ struct FdwRoutine *fdwroutine; void *fdw_private; /* 被各种扫描与连接所使用 */ List *baserestrictinfo; /* RestrictInfo结构体列表 (如果存在基础关系) */ QualCost baserestrictcost; /* 求值上述限制条件的代价 */ List *joininfo; /* RestrictInfo 结构体列表，涉及到本表的连接会用到 */ bool has_eclass_joins; /* T 意味着joininfo不完整 */ } RelOptInfo;

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73

   typedef enum RelOptKind {    RELOPT_BASEREL,    RELOPT_JOINREL,    RELOPT_OTHER_MEMBER_REL,    RELOPT_UPPER_REL,    RELOPT_DEADREL } RelOptKind;   typedef struct RelOptInfo {    NodeTag        type;    RelOptKind    reloptkind;      /* 本RelOptInfo包含的所有关系 */    Relids        relids;            /* 基本关系的ID集合 (范围表索引) */      /* 由计划器生成的预估尺寸 */    double        rows;            /* 预估结果元组数目 */      /* 计划器标记位，每个关系一份 */    bool        consider_startup;        /* 保留启动代价最低的路径？ */    bool        consider_param_startup; /* 同上, 针对参数化路径？ */    bool        consider_parallel;        /* 考虑并行路径？ */      /* 扫描当前关系的默认结果目标列表 */    struct PathTarget *reltarget;        /* Vars/Exprs, 代价, 宽度的列表 */      /* 物化相关信息 */    List       *pathlist;                /* Path 结构体列表 */    List       *ppilist;                /* pathlist中使用的ParamPathInfos */    List       *partial_pathlist;        /* 部分路径 */    struct Path *cheapest_startup_path;    struct Path *cheapest_total_path;    struct Path *cheapest_unique_path;    List        *cheapest_parameterized_paths;      /* 基础关系与连接关系都需要的 参数化信息 */    /* (参见 lateral_vars 与 lateral_referencers) */    Relids        direct_lateral_relids;    /* 直接以LATERAL方式引用的关系 */    Relids        lateral_relids;              /* 关于基础关系的信息 (连接关系不会设置这些字段！) */    Index        relid;    Oid            reltablespace;        /* 表空间 */    RTEKind        rtekind;            /* RELATION, SUBQUERY, 或 FUNCTION */    AttrNumber    min_attr;            /* 关系属性的最小值 (通常<0) */    AttrNumber    max_attr;            /* 关系属性的最大值 */    Relids           *attr_needed;        /* 被索引的数组 [min_attr .. max_attr] */    int32           *attr_widths;           /* 被索引的数组 [min_attr .. max_attr] */    List           *lateral_vars;           /* 关系所引用的LATERAL Vars 与 PHVs */    Relids        lateral_referencers;/* 侧面引用本表的关系 */    List           *indexlist;            /* IndexOptInfo列表 */    BlockNumber pages;                /* 来自pg_class的页面数估计值 */    double        tuples;    double        allvisfrac;    PlannerInfo *subroot;            /* 如有子查询 */    List           *subplan_params;     /* 如有子查询 */    int            rel_parallel_workers;    /* 期望的并行工作进程数量 */      /* 有关外部表与外部表连接的相关信息 */    Oid            serverid;        /* 外部表与外部表连接相应的服务器ID */    Oid            userid;            /* 用于检查访问权限的用户标识 */    bool        useridiscurrent;/* 当前用户是否能合法进行JOIN */    struct FdwRoutine *fdwroutine;    void           *fdw_private;      /* 被各种扫描与连接所使用 */    List           *baserestrictinfo;    /* RestrictInfo结构体列表 (如果存在基础关系) */    QualCost    baserestrictcost;    /* 求值上述限制条件的代价 */    List           *joininfo;            /* RestrictInfo 结构体列表，涉及到本表的连接会用到 */    bool        has_eclass_joins;    /* T 意味着joininfo不完整 */ } RelOptInfo;

2. 估计所有可能访问路径的代价，并将访问路径添加至RelOptInfo结构中。

   这一处理过程的细节如下：

   1. 创建一条路径，估计该路径中顺序扫描的代价，并将其写入路径中。将该路径添加到RelOptInfo结构的pathlist变量中。
   2. 如果目标表上存在相关的索引，则为每个索引创建相应的索引访问路径。估计所有索引扫描的代价，并将代价写入相应路径中。然后将索引访问路径添加到pathlist变量中。
   3. 如果可以进行位图扫描，则创建一条位图扫描访问路径。估计所有的位图扫描的代价，并将代价写入到路径中。然后将位图扫描路径添加到pathlist变量中。

3. 从RelOptInfo的pathlist中，找出代价最小的访问路径。

4. 如有必要，估计LIMIT，ORDER BY和AGGREGATE操作的代价。

为了更加清晰的理解计划器的执行过程，下面给出了两个具体的例子。

3.3.2.1 例1

首先来研究一个不带索引的简单单表查询；该查询同时包含WHERE和ORDER BY子句。

图3.10和图3.11展示了本例中计划器的处理过程。

图3.10 如何得到例1中代价最小的路径

1. 创建一个RelOptInfo结构，将其保存在PlannerInfo结构的simple_rel_array字段中。

2. 在RelOptInfo结构的baserestrictinfo字段中，添加一条WHERE子句。

   WHERE子句id<300会经由initsplan.c中定义的distribute_restrictinfo_to_rels()函数，添加至列表变量baserestrictinfo中。另外由于目标表上没有相关索引，RelOptInfo的indexlist字段为空。

3. 为了满足排序要求，planner.c中的standard_qp_callback()函数会在PlannerInfo的sor_pathkeys字段中添加一个pathkey。

   Pathkey是表示路径排序顺序的数据结构。本例因为查询包含一条ORDER BY子句，且该子句中的列为data，故data会被包装为pathkey，放入列表变量sort_pathkeys中。

4. 创建一个Path结构，并使用cost_seqscan函数估计顺序扫描的代价，并将代价写入Path中。然后使用pathnode.c中定义的add_path()函数，将该路径添加至RelOptInfo中。

   如之前所提到过的，Path中同时包含启动代价和总代价，都是由cost_seqscan函数所估计的。

在本例中，因为目标表上没有索引，计划器只估计了顺序扫描的代价，因此最小代价是自动确定的。

图3.11 如何得到例1中代价最小的路径（接图3.10）

1. 创建一个新的RelOptInfo结构，用于处理ORDER BY子句。

   本人提供Oracle(OCP、OCM)、MySQL(OCP)、PostgreSQL(PGCA、PGCE、PGCM)等数据库的培训和考证业务，私聊QQ646634621或微信db_bao，谢谢！

   注意新的RelOptInfo没有baserestrictinfo字段，该信息已经被WHERE子句所持有。

2. 创建一个排序路径，并添加到新的RelOptInfo中；然后让SortPath的subpath字段指向顺序扫描的路径。

   typedef struct SortPath { Path path; Path *subpath; /* 代表输入来源的子路径 */ } SortPath;

   1 2 3 4 5

   typedef struct SortPath {    Path    path;    Path    *subpath;        /* 代表输入来源的子路径 */ } SortPath;

   SortPath结构包含两个Path结构：path与subpath；path中存储了排序算子本身的相关信息，而subpath则指向之前得到的代价最小的路径。

   注意顺序扫描路径中parent字段，该字段指向之前的RelOptInfo结构体（也就是在baserestrictinfo中存储着WHERE子句的那个RelOptInfo）。因此在下一步创建计划树的过程中，尽管新的RelOptInfo结构并未包含baserestrictinfo，但计划器可以创建一个包含Filter的顺序扫描节点，将WHERE子句作为过滤条件。

这里已经获得了代价最小的访问路径，然后就可以基于此生成一颗计划树。3.3.3节描述了相关的细节。

3.3.2.2 例2

下面我们将研究另一个单表查询的例子，这一次表上有两个索引，而查询带有一个WHERE子句。

图3.12到3.14展示了本例中计划器的处理过程。

1. 创建一个RelOptInfo结构体

2. 在baserestrictinfo中添加一个WHERE子句；并将目标表上的索引（们）添加到indexlist中。

   在本例中，WHERE子句'id <240'会被添加至baserestrictinfo中，而两个索引：tbl_2_pkey和tbl_2_data_idx会被添加至RelOptInfo的列表变量indexlist中。

3. 创建一条路径，估计其顺序扫描代价，并添加到RelOptInfo的pathlist中。

图3.12 如何得到例2中代价最小的路径

1. 创建一个IndexPath，估计索引扫描的代价，并通过add_path()函数将IndexPath添加到RelOptInfo的pathlist中。

   在本例中有两个索引：tbl_2_pkey与tbl_2_data_index，这些索引会按先后顺序依次处理。

   一条针对tbl_2_pkey的IndexPath会先被创建出来，并进行启动代价与总代价的评估。在本例中，tbl_2_pkey是id列上的索引，而WHERE子句也包含该id列；因此WHERE子句会被存储在IndexPath的indexclauses字段中。

2. 创建另一个IndexPath，估计另一种索引扫描的代价，并将该IndexPath添加到RelOptInfo的pathlist中。

   接下来，与tbl_2_data_idx相应的IndexPath会被创建出来，并进行代价估计。本例中tbl_2_data_idx并没有相关的WHERE子句；因此其indexclauses为空。

注意add_path()函数并不总是真的会将路径添加到路径列表中。这一操作相当复杂，故这里就省去了具体描述。详细细节可以参考add_path()函数的注释。

图3.13 如何得到例2中代价最小的路径（接图3.12）

1. 创建一个新的RelOptInfo结构

2. 将代价最小的路径，添加到新RelOptInfo的pathlist中。

   本例中代价最小的路径是使用tbl_2_pkey的索引路径；故将该路径添加到新的RelOptInfo中。

图3.14 如何得到例2中代价最小的路径（接图3.13）

3.3.3 创建计划树

在最后一步中，计划器按照代价最小的路径生成一颗计划树。

计划树的根节点是定义在plannodes.h中的PlannedStmt结构，包含19个字段，其中有4个代表性字段：

• commandType存储操作的类型，诸如SELECT，UPDATE和INSERT。
• rtable存储范围表的列表（RangeTblEntry的列表）。
• relationOids存储与查询相关表的oid。
• plantree存储着一颗由计划节点组成的计划树，每个计划节点对应着一种特定操作，诸如顺序扫描，排序和索引扫描。

如上所述，计划树包含各式各样的计划节点。PlanNode是所有计划节点的基类，其他计划节点都会包含PlanNode结构。比如顺序扫描节点SeqScanNode，包含一个PlanNode和一个整型变量scanrelid。PlanNode包含14个字段。下面是7个代表性字段：

• startup_cost和total_cost是该节点对应操作的预估代价。
• rows是计划器预计扫描的行数。
• targetlist保存了该查询树中目标项的列表。
• qual储存了限定条件的列表。
• lefttree和righttree用于添加子节点。

下面是两颗计划树，分别与前一小节中的两个例子对应。

3.3.3.1 例1

第一个例子是3.3.2.1节例1对应的计划树。图3.11所示的代价最小的路径，是由一个排序路径和一个顺序扫描路径组合而成。根路径是排序路径，而其子路径为顺序扫描路径。尽管这里忽略了大量细节，但是从代价最小的路径中生成计划树的过程是显而易见的。在本例中，一个 SortNode被添加到PlannedStmt结构中，而SortNode的左子树上则挂载了一个SeqScanNode，如图3.15(a)所示。

在SortNode中，左子树lefttree指向SeqScanNode。

在SeqScanNode中，qual保存了WHERE子句：'id<300'。

图3.15. 计划树的例子

3.3.3.2 例2

第二个例子是3.3.2.2节例2对应的计划树。其代价最小的路径为索引扫描路径，如图3.14所示。因此计划树由单个IndexScanNode独立组成，如图3.15(b)所示。

在本例中，WHERE子句id < 240是一个访问谓词，它储存在IndexScanNode的indexqual字段中。

3.4 执行器如何工作

在单表查询的例子中，执行器从计划树中取出计划节点，按照自底向上的顺序进行处理，并调用节点相应的处理函数。

每个计划节点都有相应的函数，用于执行节点对应的操作。这些函数在src/backend/executor目录中。例如，执行顺序扫描的的函数（SeqScan）定义于nodeSeqscan.c中；执行索引扫描的函数（IndexScanNode）定义在nodeIndexScan.c中；SortNode节点对应的排序函数定义在nodeSort.c中，诸如此类。

当然，理解执行器如何工作的最好方式，就是阅读EXPLAIN命令的输出。因为PostgreSQL的EXPLAIN命令几乎就是照着计划树输出的。下面以3.3.3节的例1为例。

我们可以自底向上阅读EXPLAIN的结果，来看一看执行器是如何工作的。

第6行：首先，执行器通过nodeSeqscan.c中定义的函数执行顺序扫描操作。

第4行：然后，执行器通过nodeSort.c中定义的函数，对顺序扫描的结果进行排序。

临时文件

执行器在处理查询时会使用工作内存（work_mem）和临时缓冲区（temp_buffers），两者都于内存中分配。如果查询无法在内存中完成，就会用到临时文件。

使用带有Analyze选项的EXPLAIN，待解释的命令会真正执行，并显示实际结果行数，实际执行时间和实际内存用量。下面是一个具体的例子：

testdb=# EXPLAIN ANALYZE SELECT id, data FROM tbl_25m ORDER BY id; QUERY PLAN ---------------------------------------------------------------------- Sort (cost=3944070.01..3945895.01 rows=730000 width=4104) (actual time=885.648..1033.746 rows=730000 loops=1) Sort Key: id Sort Method: external sort Disk: 10000kB -> Seq Scan on tbl_25m (cost=0.00..10531.00 rows=730000 width=4104) (actual time=0.024..102.548 rows=730000 loops=1) Planning time: 1.548 ms Execution time: 1109.571 ms (6 rows)

1 2 3 4 5 6 7 8 9 10

testdb=# EXPLAIN ANALYZE SELECT id, data FROM tbl_25m ORDER BY id;                           QUERY PLAN                                                         ---------------------------------------------------------------------- Sort  (cost=3944070.01..3945895.01 rows=730000 width=4104) (actual time=885.648..1033.746 rows=730000 loops=1)    Sort Key: id    Sort Method: external sort  Disk: 10000kB    ->  Seq Scan on tbl_25m  (cost=0.00..10531.00 rows=730000 width=4104) (actual time=0.024..102.548 rows=730000 loops=1) Planning time: 1.548 ms Execution time: 1109.571 ms (6 rows)

在第6行，EXPLAIN命令显示出执行器使用了10000KB的临时文件。

临时文件会被临时创建于base/pg_tmp子目录中，并遵循如下命名规则

{"pgsql_tmp"} + {创建本文件的Postgres进程PID} . {从0开始的序列号}

1	{"pgsql_tmp"} + {创建本文件的Postgres进程PID} . {从0开始的序列号}

比如，临时文件pgsql_tmp8903.5是pid为8903的postgres进程创建的第6个临时文件

3.5 连接

PostgreSQL 中支持三种连接（JOIN）操作：嵌套循环连接（Nested Loop Join），归并连接（Merge Join） ，散列连接（Hash Join）。在PostgreSQL中，嵌套循环连接与归并连接有几种变体。

在下文中，我们会假设读者已经对这三种操作的基本行为有了解。如果读者对这些概念不熟悉，可以参阅[1, 2]。PostgreSQL支持一种针对数据倾斜的混合散列连接（hybrid hash join），关于这方面的资料不多，因此这里会详细描述该操作。

需要注意的是，这三种连接方法（join method）都支持PostgreSQL中所有的连接操作，诸如INNER JOIN，LEFT/RIGHT OUTER JOIN，FULL OUTER JOIN等；但是为了简单起见，这里只关注NATURAL INNER JOIN。

3.5.1 嵌套循环连接（Nested Loop Join）

嵌套循环连接是最为基础的连接操作，任何连接条件（join condition）都可以使用这种连接方式。PostgreSQL支持嵌套循环连接及其五种变体。

3.5.1.1 嵌套循环连接

嵌套循环连接无需任何启动代价，因此： $$ \verb|start-upcost| = 0 $$ 运行代价与内外表尺寸的乘积成比例；即$\verb|runcost|$是$O(N{\verb|outer|}× N{\verb|inner|})$，这里$N{\verb|outer|}$和$N_{\verb|inner|}$分别是外表和内表的元组条数。更准确的说，$\verb|run_cost|$的定义如下： $$ \begin{equation} \verb|run_cost|=(\verb|cpu_operator_cost|+ \verb|cpu_tuplecost|)× N{\verb|outer|}× N{\verb|inner|} + C{\verb|inner|}× N{\verb|outer|}+C{\verb|outer|} \end{equation} $$ 这里$C{\verb|outer|}$和$C{\verb|inner|}$分别是内表和外表顺序扫描的代价；

图3.16 嵌套循环连接

嵌套循环连接的代价总是会被估计，但实际中很少会使用这种连接操作，因为它有几种更高效的变体，下面将会讲到。

3.5.1.2 物化嵌套循环连接

在上面描述的嵌套循环连接中，每当读取一条外表中的元组时，都需要扫描内表中的所有元组。为每条外表元组对内表做全表扫描，这一过程代价高昂，PostgreSQL支持一种物化嵌套循环连接（materialized nested loop join） ，可以减少内表全表扫描的代价。

在运行嵌套循环连接之前，执行器会使用临时元组存储（temporary tuple storage）模块对内表进行一次扫描，将内表元组加载到工作内存或临时文件中。在处理内表元组时，临时元组存储比缓冲区管理器更为高效，特别是当所有的元组都能放入工作内存中时。

图 3.17说明了物化嵌套循环连接的处理过程。扫描物化元组在内部被称为重扫描（rescan）。

图3.17 物化嵌套循环连接

临时元组存储

PostgreSQL内部提供了临时元组存储的模块，可用于各种操作：物化表，创建混合散列连接的批次，等等。该模块包含一系列函数，都在tuplestore.c中。这些函数用于从工作内存或临时文件读写元组。使用工作内存还是临时文件取决于待存储元组的总数。

下面给出一个具体的例子，并研究一下执行器是如何处理物化嵌套循环连接的计划树并估计其代价的。

上面显示了执行器要进行的操作，执行器对这些计划节点的处理过程如下：

第7行：执行器使用顺序扫描，物化内部表tbl_b。

第4行：执行器执行嵌套循环连接操作，外表是tbl_a，内表是物化的tbl_b。

下面来估算“物化”操作（第7行）与“嵌套循环”（第4行）的代价。假设物化的内部表元组都在工作内存中。

物化（Materialize）:

物化操作没有启动代价；因此， $$ \begin{equation} \verb|start-up_cost| = 0 \end{equation} $$ 其运行代价定义如下： $$ \verb|run_cost| = 2 × \verb|cpu_operatorcost| × N{\verb|inner|}; $$ 因此： $$ \verb|run_cost|=2× 0.0025× 5000=25.0 $$ 此外， $$ \verb|total_cost| = (\verb|start-up_cost|+ \verb|total_cost_of_seq_scan|)+ \verb|run_cost| $$ 因此， $$ \verb|total_cost| = (0.0+73.0)+25.0=98.0 $$ (物化)嵌套循环:

嵌套循环没有启动代价，因此： $$ \verb|start-up_cost|=0 $$ 在估计运行代价之前，先来看一下重扫描的代价，重扫描的代价定义如下： $$ \verb|rescan_cost| = \verb|cpu_operatorcost| × N{\verb|inner|} $$ 这本例中： $$ \verb|rescan_cost| = (0.0025)× 5000=12.5 $$ 运行代价由以下公式定义： $$ \verb|run_cost| =(\verb|cpu_operator_cost| + \verb|cpu_tuplecost|)× N{\verb|inner|}× N_{\verb|outer|} \

• \verb|recancost|× (N{\verb|outer|}-1) + C^{\verb|total|}{\verb|outer|,\verb|seqscan|} + C^{\verb|total|}{\verb|materialize|}， $$ 这里 $C^{\verb|total|}{\verb|outer|,\verb|seqscan|}$代表外部表的全部扫描代价，$C^{\verb|total|}{\verb|materialize|}$代表物化代价；因此 $$ \verb|run_cost| = ( 0.0025 + 0.01 ) × 5000 × 10000 + 12.5 ×(10000−1)+145.0+98.0=750230.5 $$

3.5.1.3 索引嵌套循环连接

如果内表上有索引，且该索引能用于搜索满足连接条件的元组。那么计划器在为外表的每条元组搜索内表中的匹配元组时，会考虑使用索引进行直接搜索，以替代顺序扫描。这种变体叫做索引嵌套循环连接（indexed nested loop join），如图3.18所示。尽管这种变体叫做索引"嵌套循环连接"，但该算法基本上只需要在在外表上循环一次，因此连接操作执行起来相当高效。

图3.18 索引嵌套循环连接

下面是索引嵌套循环连接的一个具体例子。

第6行展示了访问内表中元组的代价。即在内表中查找满足第七行连接条件(id = b.id)的元组的代价。

在第7行的索引条件(id = b.id)中，b.id是连接条件中的外表属性的值。每当顺序扫描外表取回一条元组时，就会依第6行所示的索引搜索路径，查找内表中需要与之连接的元组。换而言之，外表元组的值作为参数传入内表的索引扫描中，索引扫描路径会查找满足连接条件的内表元组。这种索引路径被称为参数化（索引）路径（parameterized (index) path），细节见PostgreSQ源码：backend/optimizer/README。

该嵌套循环连接的启动代价，等于第6行中索引扫描的代价，因此： $$ \verb|start-up_cost| = 0.285 $$ 索引嵌套循环扫描的总代价由下列公式所定义： $$ \verb|total_cost|= (\verb|cpu_tuple_cost| + C^{\verb|total|}{\verb|inner,parameterized|} )× N{\verb|outer|}+C^{\verb|run|}{\verb|outer,seqscan|} $$ 这里$C^{\verb|total|}{\verb|inner,parameterized|}$是参数化内表索引扫描的整体代价，

在本例中： $$ \verb|total_cost|=(0.01+0.3625)× 5000 + 73.0 = 1935.5 $$ 而运行代价为： $$ \verb|runcost| = 1935.5-0.285=1935.215 $$ 如上所示，索引嵌套扫描的整体代价是$O(N{\verb|outer|})$。

3.5.1.4 其他变体

如果在外表上存在一个与连接条件相关的索引，那么在外表上也可以以索引扫描替代顺序扫描。特别是，当WHERE子句中的访问谓词可以使用该索引时，能缩小外表上的搜索范围，嵌套循环连接的代价可能会急剧减少。

当使用外表索引扫描时，PostgreSQL支持三种嵌套循环连接的变体，如图3.19所示。

图3.19 嵌套循环连接的三种变体，使用外表索引扫描

这些连接的EXPLAIN结果如下：

1. 使用外表索引扫描的嵌套循环连接

   testdb=# SET enable_hashjoin TO off; SET testdb=# SET enable_mergejoin TO off; SET testdb=# EXPLAIN SELECT * FROM tbl_c AS c, tbl_b AS b WHERE c.id = b.id AND c.id = 500; QUERY PLAN ------------------------------------------------------------------------------- Nested Loop (cost=0.29..93.81 rows=1 width=16) -> Index Scan using tbl_c_pkey on tbl_c c (cost=0.29..8.30 rows=1 width=8) Index Cond: (id = 500) -> Seq Scan on tbl_b b (cost=0.00..85.50 rows=1 width=8) Filter: (id = 500) (5 rows)

   1 2 3 4 5 6 7 8 9 10 11 12 13

   testdb=# SET enable_hashjoin TO off; SET testdb=# SET enable_mergejoin TO off; SET testdb=# EXPLAIN SELECT * FROM tbl_c AS c, tbl_b AS b WHERE c.id = b.id AND c.id = 500;                                   QUERY PLAN                                   ------------------------------------------------------------------------------- Nested Loop  (cost=0.29..93.81 rows=1 width=16)   ->  Index Scan using tbl_c_pkey on tbl_c c  (cost=0.29..8.30 rows=1 width=8)         Index Cond: (id = 500)   ->  Seq Scan on tbl_b b  (cost=0.00..85.50 rows=1 width=8)         Filter: (id = 500) (5 rows)

2. 使用外表索引扫描的物化嵌套循环连接

   testdb=# SET enable_hashjoin TO off; SET testdb=# SET enable_mergejoin TO off; SET testdb=# EXPLAIN SELECT * FROM tbl_c AS c, tbl_b AS b WHERE c.id = b.id AND c.id < 40 AND b.id < 10; QUERY PLAN ------------------------------------------------------------------------------- Nested Loop (cost=0.29..99.76 rows=1 width=16) Join Filter: (c.id = b.id) -> Index Scan using tbl_c_pkey on tbl_c c (cost=0.29..8.97 rows=39 width=8) Index Cond: (id < 40) -> Materialize (cost=0.00..85.55 rows=9 width=8) -> Seq Scan on tbl_b b (cost=0.00..85.50 rows=9 width=8) Filter: (id < 10) (7 rows)

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

   testdb=# SET enable_hashjoin TO off; SET testdb=# SET enable_mergejoin TO off; SET testdb=# EXPLAIN SELECT * FROM tbl_c AS c, tbl_b AS b WHERE c.id = b.id AND c.id < 40 AND b.id < 10;                                   QUERY PLAN                                     ------------------------------------------------------------------------------- Nested Loop  (cost=0.29..99.76 rows=1 width=16)   Join Filter: (c.id = b.id)   ->  Index Scan using tbl_c_pkey on tbl_c c  (cost=0.29..8.97 rows=39 width=8)         Index Cond: (id < 40)   ->  Materialize  (cost=0.00..85.55 rows=9 width=8)         ->  Seq Scan on tbl_b b  (cost=0.00..85.50 rows=9 width=8)               Filter: (id < 10) (7 rows)

3. 使用外表索引扫描的索引嵌套循环连接

   testdb=# SET enable_hashjoin TO off; SET testdb=# SET enable_mergejoin TO off; SET testdb=# EXPLAIN SELECT * FROM tbl_a AS a, tbl_d AS d WHERE a.id = d.id AND a.id < 40; QUERY PLAN ------------------------------------------------------------------------------- Nested Loop (cost=0.57..173.06 rows=20 width=16) -> Index Scan using tbl_a_pkey on tbl_a a (cost=0.29..8.97 rows=39 width=8) Index Cond: (id < 40) -> Index Scan using tbl_d_pkey on tbl_d d (cost=0.28..4.20 rows=1 width=8) Index Cond: (id = a.id) (5 rows)

   1 2 3 4 5 6 7 8 9 10 11 12 13

   testdb=# SET enable_hashjoin TO off; SET testdb=# SET enable_mergejoin TO off; SET testdb=# EXPLAIN SELECT * FROM tbl_a AS a, tbl_d AS d WHERE a.id = d.id AND a.id <  40;                                   QUERY PLAN                                     ------------------------------------------------------------------------------- Nested Loop  (cost=0.57..173.06 rows=20 width=16)   ->  Index Scan using tbl_a_pkey on tbl_a a  (cost=0.29..8.97 rows=39 width=8)         Index Cond: (id < 40)   ->  Index Scan using tbl_d_pkey on tbl_d d  (cost=0.28..4.20 rows=1 width=8)         Index Cond: (id = a.id) (5 rows)

3.5.2 归并连接（Merge Join）

与嵌套循环连接不同的是，归并连接（Merge Join）只能用于自然连接与等值连接。

函数initial_cost_mergejoin()和final_cost_mergejoin()用于估计归并连接的代价。

因为精确估计归并连接的代价非常复杂，因此这里略过不提，只会说明归并连接算法的工作流程。归并连接的启动成本是内表与外表排序成本之和，因此其启动成本为： $$ O(N_{\verb|outer|} \log2(N{\verb|outer|}) + N_{\verb|inner|} \log2(N{\verb|inner|})) $$ 这里$N{\verb|outer|}$和$N{\verb|inner|}$是分别是外表和内表的元组条数，而运行代价是$O(N{\verb|outer|}+N{\verb|inner|})$。

与嵌套循环连接类似，归并连接在PostgreSQL中有4种变体。

3.5.2.1 归并连接

图3.20是归并连接的概念示意图。

图3.20 归并连接

如果所有元组都可以存储在内存中，那么排序操作就能在内存中进行，否则会使用临时文件。

下面是一个具体的例子，一个归并连接的EXPLAIN输出如下所示。

• 第9行：执行器对内表tbl_b进行排序，使用顺序扫描（第11行）。
• 第6行：执行器对外表tbl_a进行排序，使用顺序扫描（第8行）。
• 第4行：执行器执行归并连接操作，外表是排好序的tbl_a，内表是排好序的tbl_b。

3.5.2.2 物化归并连接

与嵌套循环连接类似，归并连接还支持物化归并连接（Materialized Merge Join），物化内表，使内表扫描更为高效。

图3.21 物化归并连接

这里是物化归并连接的EXPLAIN结果，很容易发现，与普通归并连接的差异是第9行：Materialize。

• 第10行：执行器对内表tbl_b进行排序，使用顺序扫描（第12行）。
• 第9行：执行器对tbl_b排好序的结果进行物化。
• 第6行：执行器对外表tbl_a进行排序，使用顺序扫描（第8行）。
• 第4行：执行器执行归并连接操作，外表是排好序的tbl_a，内表是物化的排好序的tbl_b。

3.5.2.3 其他变体

与嵌套循环连接类似，当外表上可以进行索引扫描时，归并连接也存在相应的变体。

图3.22 归并连接的三种变体，使用外表索引扫描

这些连接的EXPLAIN结果如下。

1. 使用外表索引扫描的归并连接

   testdb=# SET enable_hashjoin TO off; SET testdb=# SET enable_nestloop TO off; SET testdb=# EXPLAIN SELECT * FROM tbl_c AS c, tbl_b AS b WHERE c.id = b.id AND b.id < 1000; QUERY PLAN ------------------------------------------------------------------------------ Merge Join (cost=135.61..322.11 rows=1000 width=16) Merge Cond: (c.id = b.id) -> Index Scan using tbl_c_pkey on tbl_c c (cost=0.29..318.29 rows=10000 width=8) -> Sort (cost=135.33..137.83 rows=1000 width=8) Sort Key: b.id -> Seq Scan on tbl_b b (cost=0.00..85.50 rows=1000 width=8) Filter: (id < 1000) (7 rows)

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

   testdb=# SET enable_hashjoin TO off; SET testdb=# SET enable_nestloop TO off; SET testdb=# EXPLAIN SELECT * FROM tbl_c AS c, tbl_b AS b WHERE c.id = b.id AND b.id < 1000;                                      QUERY PLAN                                       ------------------------------------------------------------------------------ Merge Join  (cost=135.61..322.11 rows=1000 width=16)   Merge Cond: (c.id = b.id)   ->  Index Scan using tbl_c_pkey on tbl_c c  (cost=0.29..318.29 rows=10000 width=8)   ->  Sort  (cost=135.33..137.83 rows=1000 width=8)         Sort Key: b.id         ->  Seq Scan on tbl_b b  (cost=0.00..85.50 rows=1000 width=8)               Filter: (id < 1000) (7 rows)

2. 使用外表索引扫描的物化归并连接

   testdb=# SET enable_hashjoin TO off; SET testdb=# SET enable_nestloop TO off; SET testdb=# EXPLAIN SELECT * FROM tbl_c AS c, tbl_b AS b WHERE c.id = b.id AND b.id < 4500; QUERY PLAN ------------------------------------------------------------------------------- Merge Join (cost=421.84..672.09 rows=4500 width=16) Merge Cond: (c.id = b.id) -> Index Scan using tbl_c_pkey on tbl_c c (cost=0.29..318.29 rows=10000 width=8) -> Materialize (cost=421.55..444.05 rows=4500 width=8) -> Sort (cost=421.55..432.80 rows=4500 width=8) Sort Key: b.id -> Seq Scan on tbl_b b (cost=0.00..85.50 rows=4500 width=8) Filter: (id < 4500) (8 rows)

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

   testdb=# SET enable_hashjoin TO off; SET testdb=# SET enable_nestloop TO off; SET testdb=# EXPLAIN SELECT * FROM tbl_c AS c, tbl_b AS b WHERE c.id = b.id AND b.id < 4500;                                      QUERY PLAN                                       ------------------------------------------------------------------------------- Merge Join  (cost=421.84..672.09 rows=4500 width=16)   Merge Cond: (c.id = b.id)   ->  Index Scan using tbl_c_pkey on tbl_c c  (cost=0.29..318.29 rows=10000 width=8)   ->  Materialize  (cost=421.55..444.05 rows=4500 width=8)         ->  Sort  (cost=421.55..432.80 rows=4500 width=8)               Sort Key: b.id               ->  Seq Scan on tbl_b b  (cost=0.00..85.50 rows=4500 width=8)                     Filter: (id < 4500) (8 rows)

3. 使用外表索引扫描的索引归并连接

   testdb=# SET enable_hashjoin TO off; SET testdb=# SET enable_nestloop TO off; SET testdb=# EXPLAIN SELECT * FROM tbl_c AS c, tbl_d AS d WHERE c.id = d.id AND d.id < 1000; QUERY PLAN ------------------------------------------------------------------------------- Merge Join (cost=0.57..226.07 rows=1000 width=16) Merge Cond: (c.id = d.id) -> Index Scan using tbl_c_pkey on tbl_c c (cost=0.29..318.29 rows=10000 width=8) -> Index Scan using tbl_d_pkey on tbl_d d (cost=0.28..41.78 rows=1000 width=8) Index Cond: (id < 1000) (5 rows)

   1 2 3 4 5 6 7 8 9 10 11 12 13

   testdb=# SET enable_hashjoin TO off; SET testdb=# SET enable_nestloop TO off; SET testdb=# EXPLAIN SELECT * FROM tbl_c AS c, tbl_d AS d WHERE c.id = d.id AND d.id < 1000;                                      QUERY PLAN                                       ------------------------------------------------------------------------------- Merge Join  (cost=0.57..226.07 rows=1000 width=16)   Merge Cond: (c.id = d.id)   ->  Index Scan using tbl_c_pkey on tbl_c c  (cost=0.29..318.29 rows=10000 width=8)   ->  Index Scan using tbl_d_pkey on tbl_d d  (cost=0.28..41.78 rows=1000 width=8)         Index Cond: (id < 1000) (5 rows)

3.5.3 散列连接（Hash Join）

与归并连接类似，散列连接（Hash Join）只能用于自然连接与等值连接。

PostgreSQL中的散列连接的行为因表的大小而异。 如果目标表足够小（确切地讲，内表大小不超过工作内存的25％），那么散列连接就是简单的两阶段内存散列连接（two-phase in-memory hash join） ； 否则，将会使用带倾斜批次的混合散列连接（hybrid hash join）。

本小节将介绍PostgreSQL中这两种散列连接的执行过程。

这里省略了代价估算的部分，因为它很复杂。粗略来说，假设向散列表插入与搜索时没有遇到冲突，那么启动和运行成本复杂度都是$O(N{\verb|outer|} + N{\verb|inner|})$。

3.5.3.1 内存散列连接

下面将描述内存中的散列连接。

内存中的散列连接是在work_mem中处理的，在PostgreSQL中，散列表区域被称作处理批次（batch）。 一个处理批次会有多个散列槽(hash slots)\，内部称其为桶（buckets），桶的数量由nodeHash.c中定义的ExecChooseHashTableSize()函数所确定。 桶的数量总是2的整数次幂。

内存散列连接有两个阶段：构建（build）阶段和探测（probe）阶段。 在构建阶段，内表中的所有元组都会被插入到batch中；在探测阶段，每条外表元组都会与处理批次中的内表元组比较，如果满足连接条件，则将两条元组连接起来。

为了理解该操作的过程，下面是一个具体的例子。 假设该查询中的连接操作使用散列连接。

散列连接的过程如图3.23和3.24所示。

图3.23 内存散列连接的构建阶段

1. 在工作内存上创建一个处理批次。

   在本例中，处理批次有八个桶；即桶的数量是2的3次方。

2. 将内表的第一个元组插入批次的相应的桶中。

   具体过程如下：

   1. 找出元组中涉及连接条件的属性，计算其散列键。

      在本例中，因为WHERE子句是inner.attr1 = outer.attr2，因此内置的散列函数会对第一条元组的属性attr1取散列值，用作散列键。

   2. 将第一条元组插入散列键相应的桶中。

      假设第一条元组的散列键以二进制记法表示为0x000 ... 001，即其末三位（bit）为001。 在这种情况下，该元组会被插入到键为001的桶中。

   在本文中，构建处理批次的插入操作会用运算符 ⊕ 表示。

3. 插入内表中的其余元组。

图3.24. 内存散列连接的探测阶段

1. 依外表的第一条元组进行探测。

   详情如下：

   1. 找出第一条外表元组中涉及连接条件的属性，计算其散列键。

      在这个例子中，假设第一条元组的属性attr2的散列键是0x000 ... 100，即其末三位（bit）为100。 最后三位是100。

   2. 将外表中第一条元组与批次中的内表元组进行比较。如果满足连接条件，则连接内外表元组。

      因为第一个元组的散列键的末三位为100，执行器找出键为100的桶中的所有内表元组，并对内外表元组两侧相应的属性进行比较。这些属性由连接条件（在WHERE子句中）所指明。

      如果满足连接条件，执行器会连接外表中的第一条元组与内表中的相应元组。如果不满足则执行器不做任何事情。

      在本例中，键为100的桶中有Tuple_C。如果Tuple_C的attr1等于第一条元组（Tuple_W）的attr2，则Tuple_C和Tuple_W将被连接，并保存至内存或临时文件中。

   在本文中，处理批次的探测操作用运算符 ⊗ 表示。

2. 依次对外表中的其他元组执行探测。

3.5.3.2 带倾斜的混合散列连接

当内表的元组无法全部存储在工作内存中的单个处理批次时，PostgreSQL使用带倾斜批次的混合散列连接算法，该算法是混合散列连接的一种变体。

首先，这里会描述混合散列连接的基本概念。在第一个构建和探测阶段，PostgreSQL准备多个批次。与桶的数目类似，处理批次的数目由函数ExecChooseHashTableSize()决定，也总是2的整数次幂。工作内存中只会分配一个处理批次，而其他批次作都以临时文件的形式创建。属于这些批次的元组将通过临时元组存储功能，被写入到相应的文件中。

图3.25说明了如何将元组存储在四个（$ 2 ^ 2 $）处理批次中。在本例中元组散列键的最后五个比特位决定了元组所属的批次与桶，因为处理批次的数量为$2^2$，而桶的数量为$2^3$，因此需要5个比特位来表示，其中前两位决定了元组所属的批次，而后三位决定了元组在该批次中所属的桶。例如：Batch_0存储着散列键介于$\textcolor{red}{00}000$与$\textcolor{red}{00}111$的元组；而Batch_1存储着散列键介于$\textcolor{red}{01}000$与$\textcolor{red}{01}111$的元组，依此类推。

图3.25 混合散列连接中的多个处理批次

在混合散列连接中，构建与探测阶段的执行次数与处理批次的数目相同，因为内外表元组都被存至相同数量的处理批次中。在第一轮构建与探测阶段中，除了处理第一个处理批次，还会创建所有的处理批次。另一方面，第二轮及后续的处理批次都需要读写临时文件，这属于代价巨大的操作。因此PostgreSQL还准备了一个名为skew的特殊处理批次，即倾斜批次，以便在第一轮中高效处理尽可能多的元组。

这个特殊的倾斜批次中的内表元组在连接条件内表一侧属性上的取值，会选用外表连接属性上的高频值（MCV）。因此在第一轮处理中能与外表中尽可能多的元组相连接。这种解释不太好理解，因此下面给出了一个具体的例子。

假设有两个表：客户表customers与购买历史表purchase_history。customers由两个属性组成：name和address； purchase_history由两个属性组成：customer_name和buying_item。customers有10,000行，而purchase_history表有1,000,000行。前10％的客户进行了70％的购买。

理解了这些假设，让我们考虑当执行以下查询时，带倾斜的混合散列连接的第一轮是如何执行的。

如果customers是内表，而purchase_history是外表，则PostgreSQL将使用purchase_history表的高频值值，将前10％的customers元组存储于倾斜批次中。 请注意这里引用的是外表上的高频值，而插入倾斜批次的是内表元组。 在第一轮的探测阶段，外表（purchase_history）中70％的元组将与倾斜批次中存储的元组相连接。 因此，外表分布越是不均匀，第一轮中越是可以处理尽可能多的元组。

接下来会介绍带倾斜批次的混合散列连接的工作原理，如图3.26至3.29所示。

图3.26 混合散列连接的构建阶段的第一轮

1. 在工作内存中创建一个处理批次，以及一个倾斜批次。

2. 创建处理批次相应的临时文件，用于存储排好序的内表元组。

   在本例中，内表被分割为四个批次，因此创建了三个批次文件。

3. 为内表的第一条元组执行构建操作。

   细节如下：

   1. 如果第一条元组应当插入倾斜批次中，则将其插入倾斜批次；否则继续下一步。

      在该例中，如果第一条元组属于前10％的客户，则将其插入到倾斜批次中。

   2. 计算第一条元组的散列键，然后将其插入相应的处理批次。

4. 对内表其余元组依次执行构建操作。

图3.27 混合散列连接，探测阶段第一轮

1. 创建临时处理批次文件，用于外表排序。

2. 为外表的第一条元组执行探测操作，如果外表第一条元组上相应字段取值为MCV，则在倾斜批次上进行探测，否则进行第七步。

   在本例中，如果第一条元组是前10％客户的购买数据，则它会与倾斜批次中的内表元组进行比较。

3. 为外表的第一条元组执行探测操作。

   操作的内容取决于该元组散列键的取值。如果该元组属于Batch_0则直接完成探测操作；否则将其插入相应的外表处理批次中。

4. 为外表的其余元组执行探测操作。

   注意在本例中，外表中70％的元组已经在第一轮中的倾斜批次中处理了。

图3.28 构建阶段与探测阶段，第二轮

1. 移除倾斜批次与Batch_0，为下一轮处理批次腾地方。
2. 为批次文件batch_1_in中的内表元组执行构建操作。
3. 为批次文件batch_1_out中的外表元组依次执行探测操作。

图3.29 构建阶段与探测阶段，第三轮及后续

1. 为批次文件batch_2_in与batch_2_out执行构建操作与探测操作。
2. 为批次文件batch_3_in与batch_3_out执行构建操作与探测操作。

3.5.4 连接访问路径与连接节点

3.5.4.1 连接访问路径

嵌套循环连接的访问路径由JoinPath结构表示，其他连接访问路径，诸如MergePath与HashPath都基于其实现。

下图列出了所有的连接访问路径，细节略过不提。

图3.30 Join访问路径